12:58 - 27.06 Bem, assim como a maioria dos conteúdos que estou fazendo por enquanto minha inicial preocupação é que tenha ao menos o conteúdo básico e aos poucos vou complementando, nosso conteúdo foco do dia em matemática será: Conjuntos. O importante que devemos compreender sobre conjuntos é sua contextualização, é algo bastante "tocável", pois pode fazer parte facilmente do nosso cotidiano, existe uma necessidade nata do ser humano de agrupar, de ordenar e é isso que esse conteúdo faz.
Começaremos pela Teoria elementar dos Conjuntos Quando pensamos em conjuntos a primeira coisa que devemos saber é o que são CONJUNTOS
DEFINIÇÃO: É o agrupamento de elementos com características comuns
O nome dos conjuntos sempre serão dados por uma letra maiúscula do alfabeto, por exemplo: A, B , C ... Z. Eles representam um agrupamento de coisas como por exemplo, um conjunto de estados brasileiros que seriam formados A = {Amazonas, Pará, Roraima, Rondônia, Acre, Tocantins,...}
Olhando no mapa os estados que pertencem ao conjunto poderemos ver que Tocantins faz parte do conjunto de estados brasileiros, a notação que utilizamos para descrever que algum elemento faz parte é o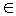 (lê-se pertence), logo Tocantis
(lê-se pertence), logo Tocantis 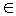 ao conjunto A.
ao conjunto A.
Olhando no mapa os estados que pertencem ao conjunto poderemos ver que Tocantins faz parte do conjunto de estados brasileiros, a notação que utilizamos para descrever que algum elemento faz parte é o
As principais formas de descrever um conjunto são as seguintes:
Por extenso: A={0,1,2,3..}
Por descrição: P={x|x é par}
Por diagrama de Venn- Euler

Outra coisa que devemos saber sobre os conjuntos é que ele pode ser formado por um número finito ( que dizer que ele tem fim) de elementos ou infinito ( que dizer que ele não tem fim) de elementos.
Ele pode ser unitário - o próprio nome já diz - formado por um único elemento : Y = {x|x é par e primo} = {2}
Pode ser vazio - caso não tenha nenhum elemento com a característica procurada: W={x|x é par e ímpar}
Alguns símbolos que precisa compreender:
| N: conjunto dos números naturais | |
| Z : conjunto dos números inteiros | |
| / : tal que | Q: conjunto dos números racionais |
| Q'= I: conjunto dos números irracionais | |
| R: conjunto dos números reais |
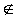 (não pertence) esse simbolo serve para representar que um certo elemento não pertence a um determinado conjunto. por exemplo. A = { a, b, c, d} , logo a letra f
(não pertence) esse simbolo serve para representar que um certo elemento não pertence a um determinado conjunto. por exemplo. A = { a, b, c, d} , logo a letra f 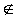 A
A
Conjunto dos Números Naturais
Conjunto dos Números Inteiros
Note também que 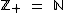 e que
e que 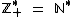 .
.
Conjunto dos Números Racionais
O conjunto dos número racionais é representado pela letra Q ( 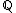 ).
).
Conjunto dos Números Irracionais
A letra I ( 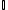 ) representa o conjunto dos número irracionais.
) representa o conjunto dos número irracionais.
Conjunto dos Números Reais
número natural também é um número inteiro ( 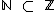 ), assim como um número inteiro também é um número racional (
), assim como um número inteiro também é um número racional ( 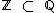 ), portanto
), portanto 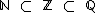 .
.
Vimos também que os números racionais não estão contidos no conjunto dos números irracionais e vice-versa. A intersecção destes conjuntos resulta no conjunto vazio: 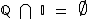
A intersecção é uma operação por meio da qual obtemos um conjunto de todos os elementos que pertencem simultaneamente a todos os conjuntos envolvidos. Sejam dois conjuntos 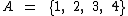 e
e 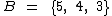 , a intersecção entre estes dois conjuntos será
, a intersecção entre estes dois conjuntos será 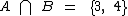 .
.
O conjunto dos números reais é representado pela letra R ( 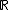 ) e é formado pela união do conjunto dos números racionais com o conjunto dos irracionais, que simbólicamente representamos por:
) e é formado pela união do conjunto dos números racionais com o conjunto dos irracionais, que simbólicamente representamos por: 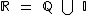 .
.
A união é uma operação por meio da qual obtemos um conjunto de todos os elementos que pertencem ao menos a um dos conjuntos envolvidos. Sejam dois conjuntos 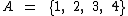 e
e 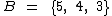 , a união entre estes dois conjuntos será
, a união entre estes dois conjuntos será 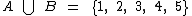 .
.
O conjunto dos números racionais está contido no conjunto dos números reais ( 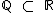 ), assim como o conjunto dos números irracionais também é subconjunto do conjunto dos números reais (
), assim como o conjunto dos números irracionais também é subconjunto do conjunto dos números reais ( 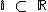 ).
).
Através dos caracteres especiais "+" e "*", por exemplo, podemos representar o conjunto dos números reais positivos por 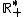 .
.
Abaixo temos um exemplo de conjunto contendo número reais:
Conjunto vazio: é um conjunto que não possui elementos. O conjunto vazio é representado por { } ou  .
.
- Subconjuntos: quando todos os elementos de um conjunto A qualquer pertencem a um outro conjunto B, diz-se, então, que A é um subconjunto de B, ou seja A
- Todo o conjunto A é subconjunto dele próprio, ou seja
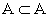 ;
; - O conjunto vazio, por convenção, é subconjunto de qualquer conjunto, ou seja
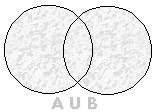
União de Conjuntos: dados os conjuntos A e B, define-se como união dos conjuntos A e B ao conjunto representado por
Intersecção de Conjuntos: dados os conjuntos A e B, define-se como intersecção dos conjuntos A e B ao conjunto representado por  , formado por todos os elementos pertencentes a A e B, simultaneamente, ou seja:
, formado por todos os elementos pertencentes a A e B, simultaneamente, ou seja: 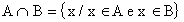
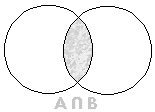
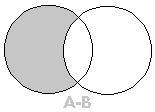
Diferença de Conjuntos: dados os conjuntos A e B, define-se como diferença entre A e B (nesta ordem) ao conjunto representado por A-B, formado por todos os elementos pertencentes a A, mas que não pertencem a B, ou seja 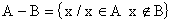
Propriedades da relação ⊆
esse símbolo é o "estar contido"
A relação de inclusãoo de conjuntos ⊆ obedece as seguintes propriedades. Para quaisquer X, Y e Z,
(Reflexiva) X ⊆ X - ou seja, um elemento sempre está contido nele mesmo,
(transitiva) X ⊆ Y e Y ⊆ Z =⇒ X ⊆ Z , se X está contido em Y, e Y está contido em Z, logo X está contido em Z.
I3. (anti-simétrica) X ⊆ Y e Y ⊆ X =⇒ X = Y - se X está contido em Y e Y está contido em X, logo X é igual a Y.
∅ ⊆ X o vazio está contido em X,
X ⊆ U X está contido do Conjunto Universo.












