12. Geometria espacial: retas, planos e suas posições relativas no espaço; poliedros regulares; prismas e pirâmides e respectivos troncos; cilindros, cones e esferas; cálculo de áreas e volumes.
me organizando
A Geometria espacial (euclidiana) funciona como uma ampliação da
Geometria plana (euclidiana) e trata dos métodos apropriados para o
estudo de objetos espaciais assim como a relação entre esses
elementos. Os objetos primitivos do ponto de vista espacial, são:
pontos, retas, segmentos de retas, planos, curvas, ângulos e
superfícies. Os principais tipos de cálculos que podemos realizar são:
comprimentos de curvas, áreas de superfícies e volumes de regiões
sólidas. Tomaremos ponto e reta como conceitos primitivos, os quais
serão aceitos sem definição.
Um plano é um subconjunto do espaço R3 de tal modo que quaisquer dois pontos desse conjunto podem ser ligados por um segmento de reta inteiramente contido no conjunto. Um plano no espaço R3 pode ser determinado por qualquer uma das situações:
!" Três pontos não colineares (não pertencentes à mesma reta);
!" Um ponto e uma reta que não contem o ponto;
!" Um ponto e um segmento de reta que não contem o ponto;
!" Duas retas paralelas que não se sobrepõe;
!" Dois segmentos de reta paralelos que não se sobrepõe;
!" Duas retas concorrentes;
!" Dois segmentos de reta concorrentes.
Duas retas (segmentos de reta) no espaço R³ podem ser: paralelas, concorrentes ou reversas.
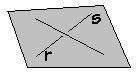
Duas retas são ditas reversas quando uma não tem interseção com a outra e elas não são paralelas. Pode-se pensar de uma rera r desenhada no chão de uma casa e uma reta s desenhada no teto dessa mesma casa.
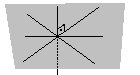
Uma reta é perpendicular a um plano no espaço R³, se ela intersecta o plano em um ponto P e todo segmento de reta contido no plano que tem P como uma de suas extremidades é perpendicular à reta.
Uma reta r é paralela a um plano no espaço R³ , se existe uma reta s inteiramente contida no plano que é paralela à reta dada. Seja P um ponto localizado fora de um plano. A distância do ponto ao plano é a medida do segmento de reta perpendicular ao plano em que uma extremidade é o ponto P e a outra extremidade é o ponto que é a interseção entre o plano e o segmento.
Se o ponto P estiver no plano, a distância é nula. Planos concorrentes no espaço R3
são planos cuja interseção é uma reta. Planos paralelos no espaço R3 são planos que não tem interseção.
Quando dois planos são concorrentes, dizemos que tais planos formam um diedro e o ângulo
formado entre estes dois planos é denominado ângulo diedral. Para obter este ângulo diedral,
basta tomar o ângulo formado por quaisquer duas retas perpendiculares aos planos concorrentes. Planos normais são aqueles cujo ângulo diedral é um ângulo reto
(90 graus).











