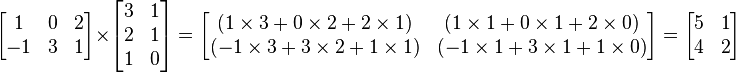8. Matrizes: operações, propriedades, inversa. Determinantes e propriedades. Matriz associada a um sistema de equações lineares; resolução e discussão

12:23  , , ,  





8. Matrizes: operações, propriedades, inversa. Determinantes e propriedades. Matriz associada a um sistema de equações lineares; resolução e discussão de sistemas lineares.

17:54 29.07 Boa tarde/noite hoje falaremos sobre um dos assuntos que eu mais gosto em matemática, já peguei tantos livros sobre e fiz tantas questões que eu realmente tenho um amor todo especial por esse conteúdo. Matrizes é algo realmente fantástico e é algo que realmente precisamos compreender e pronto.


Iniciaremos pela parte mais lógica da explicação, saberemos agora o que é uma matriz que nada mais é uma forma representativa, organizada em linhas e colunas e que é aplicada principalmente em sistemas operacionais, funcionando para ajudar a engenharia, matemática e muitas outras que regem o mundo. rs,

DEFINIÇÃO: Dados dois números m e n naturais e não nulos, chama-se matriz m por n (indica-se mxn) toda a tabela M formado por números reais distribuídos em m linhas e n colunas.

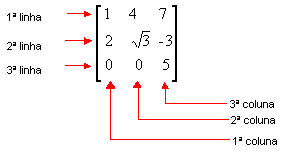
Abaixo tem um exemplo de representação de uma matriz comum, na qual temos a posição das linhas e quais seriam as colunas.


Comumente chamamos cada elemento de uma matriz, de aij, no qual o i representa qual linha estamos nos referindo e o j qual coluna. Com a convenção de que as linhas sejam numeradas de cima para baixo e as colunas da esquerda para direita. (como mostra a figura acima)

Uma matriz M do tipo mxn pode também ser indicada por M = (aij); i E {1, 2, 3, 4, ..., m} e j E {1, 2, 3 ,4 ..., n}, ou simplesmente M = (aij) mxn



A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix}


Matrizes especiais

1. Matriz linha é toda matriz do tipo 1 x n, ou seja formada apenas por 1 linha.

Página 3

2. Matriz Coluna é toda matriz do tipo m x 1, ou seja formada apenas por 1 coluna.

Página 3

3. Matriz nula é toda matriz em que todos seus elementos são nulos, ou seja, iguais a zero.


Igualdade entre matrizes.

Da forma mais prática possível duas matrizes são iguais quando todos os elementos da primeira matriz são iguais a todos os elementos da segunda matriz
Vamos observar a matriz abaixo:



Percebemos que ambas são formadas por 3 linhas e duas colunas, o primeiro elemento o a11 de ambas é igual a -50, o a12 é igual a 11 e assim acontece com todos elementos, logo dizemos que a matriz A é igual a matriz B. Matriz identidade

I_{2} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}.

Matriz Transposta

A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}, A^t = \begin{bmatrix} 1 & 4 \\ 2 & 5 \\ 3 & 6 \end{bmatrix}
Multiplicação envolvendo escalar

2 \begin{bmatrix} 1 & 8 & -3 \\ 4 & -2 & 5 \end{bmatrix} = \begin{bmatrix} 2\times 1 & 2\times 8 & 2\times -3 \\ 2\times 4 & 2\times -2 & 2\times 5 \end{bmatrix} = \begin{bmatrix} 2 & 16 & -6 \\ 8 & -4 & 10 \end{bmatrix}

Adição e subtração de matrizes


\begin{bmatrix} 1 & 3 & 2 \\ 1 & 0 & 0 \\ 1 & 2 & 2 \end{bmatrix} + \begin{bmatrix} 0 & 0 & 5 \\ 7 & 5 & 0 \\ 2 & 1 & 1 \end{bmatrix} = \begin{bmatrix} 1+0 & 3+0 & 2+5 \\ 1+7 & 0+5 & 0+0 \\ 1+2 & 2+1 & 2+1 \end{bmatrix} = \begin{bmatrix} 1 & 3 & 7 \\ 8 & 5 & 0 \\ 3 & 3 & 3 \end{bmatrix}


Multiplicação de matrizes

(AB)[i,j] = A[i,1] B[1,j] + A[i,2] B[2,j] + ... + A[i,n] B[n,j]

\begin{bmatrix} 1 & 0 & 2 \\ -1 & 3 & 1 \\ \end{bmatrix} \times \begin{bmatrix} 3 & 1 \\ 2 & 1 \\ 1 & 0 \end{bmatrix} = \begin{bmatrix} (1 \times 3 + 0 \times 2 + 2 \times 1) & (1 \times 1 + 0 \times 1 + 2 \times 0) \\ (-1 \times 3 + 3 \times 2 + 1 \times 1) & (-1 \times 1 + 3 \times 1 + 1 \times 0) \\ \end{bmatrix} = \begin{bmatrix} 5 & 1 \\ 4 & 2 \\ \end{bmatrix}